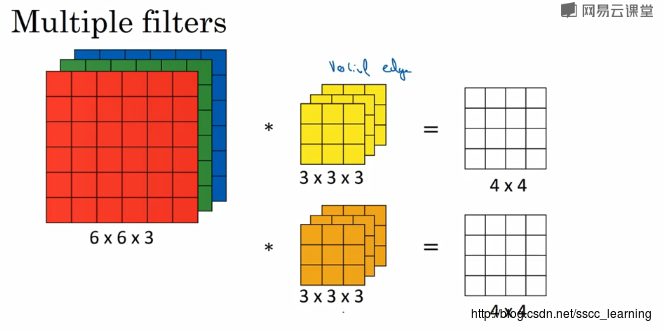
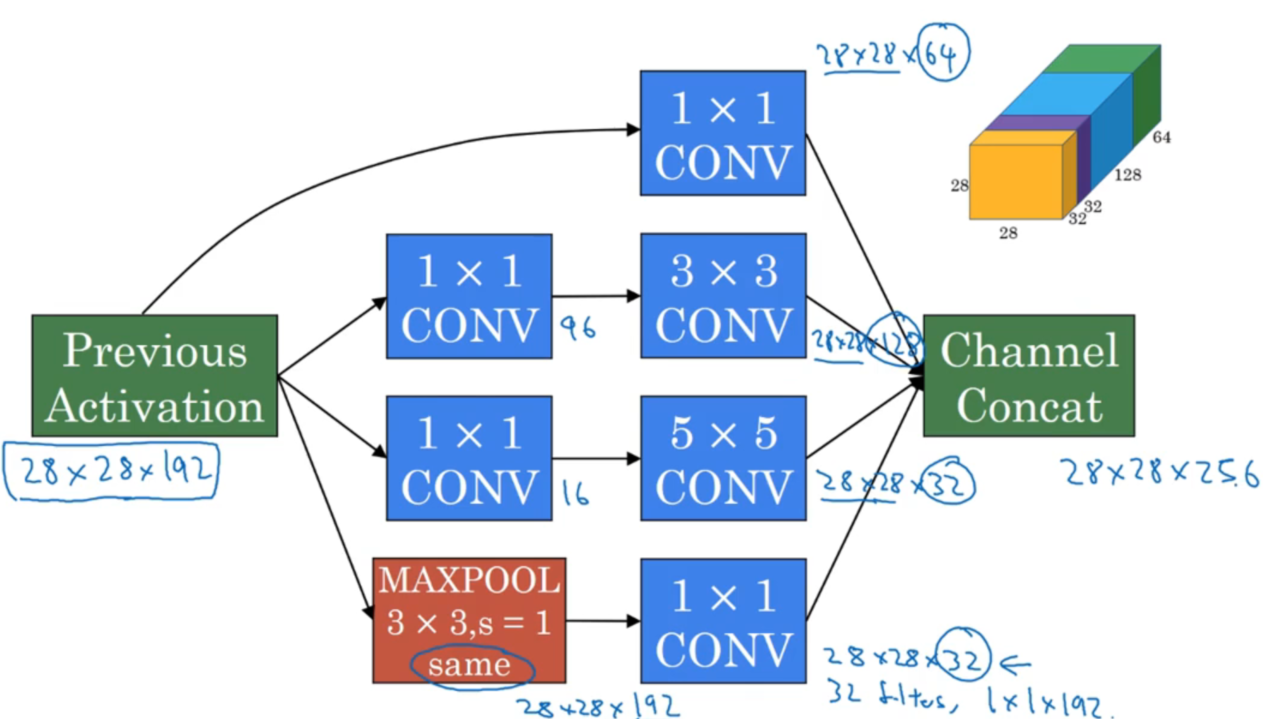
【统计学习方法笔记01】统计学习概论
一、统计学习
1.1 统计学习的概念
(1)概念
统计学习是关于计算机基于数据构建概率统计模型,并运用模型对数据进行预测与分析的一门学科。
统计学习是计算机系统通过运用数据及统计方法提高系统性能的机器学习。
(2)对象
数据,如数字、文字、图像、视频、音频等。
(3)目的
从数据出发,提取数据的特征,抽象数据的模型,发现数据的知识,最后回到数据的分析与预测中。
1.2 统计学习的分类
1.2.1 基本分类
(1)监督学习
从标注数据中学习预测模型的机器学习问题。即学习从输入到输出的映射的统计规律。
- 输入空间与输出空间:输入与输出的所有可能取值。
- 输入变量与输出变量均为连续变量,回归问题
- 输出变量为离散变量,分类问题
- 输入变量与输出变量均为变量序列,标注问题
- 特征空间:输入可以用特征向量表示,所有特征向量存在的空间。
- 联合概率分布:假设训练数据与测试数据是一句联合概率分布P(X,Y)独立同分布产生的。
- 假设空间:由输入到输出的映射的集合。
(2)无监督学习
从无标注数据中学习预测模型的机器学习问题。即学习数据的统计规律或潜在结构。
- 输入空间与输出空间:模型的输入与输出的所有可能取值的集合。
- 输入是实例,由特征向量表示。
- 输出是对输入的分析结果,由输入的类别、转换或概率表示。
- 假设空间:所有模型z=g(x)的集合,其中X是输入空间,Z是隐式结构空间。
(3)强化学习
智能系统在于环境的连续互动中学习最优行为策略的机器学习问题。智能系统观测到与环境互动得到的数据序列,本质是学习最优的序贯决策。
智能系统与环境的互动过程:每一步$t$,智能系统从环境观测到一个状态$s_t$和奖励$r_t$,采取一个动作$a_t$。环境根据智能系统的动作,确定下一步$t+1$的状态$s_{t+1}$和$r_{t+1}$。使系统实现长期累计奖励的最大化。
强化学习的马尔可夫决策过程由五元组<S, A, P, r, $\gamma$>组成:
- S:有限状态的集合
- A:有限动作的集合
- P:状态转移概率函数
- r:奖励函数
- $\gamma$:衰减系数
策略:给定状态下的动作的函数
价值函数:策略从某一个状态开始的长期累积奖励的数学期望
动作价值函数:策略从某一个状态和动作开始的长期累计奖励的数学期望
(4)半监督学习与主动学习
半监督学习:利用标注数据和未标注数据学习预测模型的机器学习问题。
主动学习:机器不断主动给出实例让教师进行标注,然后利用标注数据学习预测模型的机器学习问题。
1.2.2 按模型分类
(1)概率模型与非概率模型
- 概率模型:取条件分布形式P(y|x)
- 非概率模型:函数形式y=f(x)
(2)线性模型与非线性模型
- 线性模型:感知机、线性支持向量机、k近邻、潜在语义分析
- 非线性模型:支持向量机、神经网络
(3)参数化模型与非参数化模型
- 参数化模型:假设模型参数的维度固定,模型可以由有限维参数完全刻画
- 非参数化模型:假设模型参数的维度不固定或者无穷大,随着训练数据量的增加而不断增大
1.2.2 按算法分类
(1)在线学习
每次接受一个样本,进行预测,之后学习模型,并不断重复。
(2)批量学习
一次接受所有数据,学习模型,之后进行预测。
1.2.3 按技巧分类
(1)按贝叶斯学习
在概率模型的学习和推理中,利用贝叶斯定理,计算在给定数据条件下模型的条件概率,并应用这个原理进行模型的估计。
(2)核方法
使用核函数表示和学习非线性模型的一种机器学习方法。
二、统计学习的三要素
2.1 模型
- 概率模型:假设空间为条件概率的集合。{f|Y=f(X)}
- 非概率模型:假设空间为决策函数的集合。{P|P(Y|X)}
2.2 策略
(1)损失函数
- 0-1损失函数:$L(Y,f(x))=0,1$
- 平方损失函数:$L(Y,f(x))=(Y-f(X))^2$
- 绝对损失函数:$L(Y,f(x))=|Y-f(X)|$
- 对数损失函数:$L(Y,f(x))=-logP(Y|X)$
(2)风险函数
损失函数的平均值,或称为期望损失。
当样本容量足够大时,经验风险最小化有利于保证很好的学习效果。当样本容量较小时,学习效果未必好,可能会产生过拟合。
(3)结构风险
结构风险在经验风险上加上表示模型复杂度的正则化项。
$R(f)=\frac{1}{N}\sum^N_{i=1}L(y_i,f(x_i))+\lambda J(f)$
其中$J(f)$为模型复杂度,模型越复杂其值越大。常取L1范数$||\omega||_1$或L2范数$\frac{||\omega||^2}{2}$
$\lambda$为系数,用于权衡风险函数与模型复杂度。
结构风险的思想其实就是奥卡姆剃刀原理,即在所有可能的模型函数中,选择能够很好的解释已知数据,并且最简单的模型。
2.3 算法
三、泛化能力
泛化能力是学习到的模型对未知数据的预测能力。
五、生成模型与判别模型
极大似然估计:已知一组数据输出,定义该组数据的概率函数,通过求概率函数的极大值点,确定数据输入。