【深度学习笔记05】深度学习常用优化算法
一、Mini-batch梯度下降法
(1)为什么需要mini-batch
我们知道,在神经网络中常使用向量化的方法,来实现较快速的处理所有m个样本。
但是这样的方法,对于超大数量的样本来说,比如对于一个有100万样本的数据集,使用向量化的方法就代表将创建一个有100万列的超大矩阵,并且需要对整个数据集进行处理后才能进一步做梯度下降,这种方法称为batch梯度下降法。
为了解决这个问题,可以把训练集分割为小一些的子训练集,这些子集称为mini-batch,比如每次取出1000个样本进行训练,然后再取1000个样本训练。
(2)如何理解mini-batch
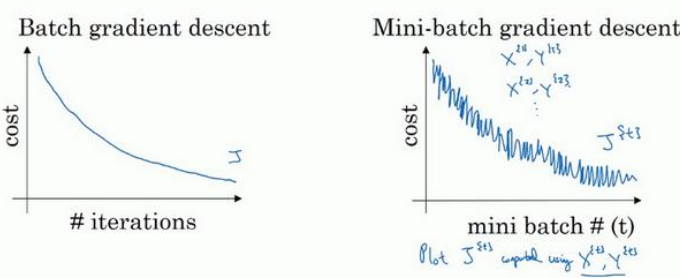
使用mini-batch梯度下降法时,每次迭代过程需要处理的是$X^$和$y^$,因此做出的成本函数图在取不同子集的过程中是不一样的,但由于权重和偏置是随着训练逐渐优化,因此整体的成本函数是震荡下降的。
(3)超参数:batch_size
在设置minibatch的过程中用到的一个超参数就是batch大小,如果训练集的大小是m的话:
- batch_size=m:mini-batch子集与整个训练集一样,其实就是batch梯度下降法,这种情况相对噪声低一些,幅度大一些,在此方法后可以继续寻找最小值。
- batch_size=1:叫做梯度下降法,每个样本都是独立的mini-batch,这种方法大部分情况下会像最小值靠近,有时会远离最小值,且有很多噪声,而且该方法永远不会手链,而是会一直在最小值附近波动。
实际工作中选择的mini-batch大小通常在两种极限情况之间,即1<batch_size<m。并且如果样本数量较小,就没必要划分子集了,直接使用batch梯度下降法即可,对于数目较大的数据,一般batch_size选择为64到512,根据电脑内存情况选取。
(4)编程实现
1 | def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0): |
二、动量梯度下降法
2.1 指数加权平均数
(1)什么是指数加权平均数
指数加权平均数,可以将震荡往复的噪声曲线拟合为一条平滑的曲线。
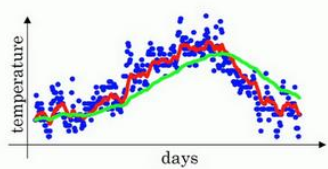
其数学表达式如下:
$V_t=\beta V_{t-1}+(1-\beta)\theta_t$
(2)如何理解指数加权平均数
以$\beta=0.9$为例,我们可以写出下面的式子
$V_{100}=0.9V_{99}+0.1\theta_{100}$
$V_{99}=0.9V_{98}+0.1\theta_{99}$
$V_{98}=0.9V_{97}+0.1\theta_{98}$
我们将后两式代入第一式就可以得到:
$V_{100}=0.9V_{99}+0.1\theta_{100}$
$=0.1\theta_{100}+0.9(0.9V_{98}+0.1\theta_{99})$
$=0.1\theta_{100}+0.9(0.1\theta_{99}+0.9(0.9V_{97}+0.1\theta_{98}))$
$=0.1\theta_{100}+0.1\times 0.9\theta_{99}+0.1\times 0.9^2\theta_{98}++0.1\times 0.9^3\theta_{97}+\dots$
可以看出来,这是一个对$\theta$的加和和平均,对于$V_{100}$来说,它由前99个数据决定,并且离100越近的数据,权重越大,离得越远的数据权重越小,权重是成指数衰减的函数。
(3)超参数:$\beta$
在公式$V_t=\beta V_{t-1}+(1-\beta)\theta_t$中,如果$\beta$较大,说明在加权过程中,权重衰减更慢,因此可以看作对更多个数据的平均。如果$\beta$较小,说明加权过程中,权重衰减更快,可以看作只对临近几个数据平均。
指数加权平均公式的好处在于,它占用极少的内存,每次只存储上一次的变量,然后计算最新的数据并不断覆盖就可以了,而不需要为了拟合曲线读入所有的数据。
2.2 动量梯度下降法
基本思想为计算梯度的加权平均数,并利用该梯度更新权重。
比如要优化某个成本函数,梯度下降的过程中总是会慢慢摆动直到下降到最小值,这样的上下波动减慢了梯度下降的速度,并且不能使用更大的学习率,因为一旦学习率过大,结果就可能会超出函数的范围。
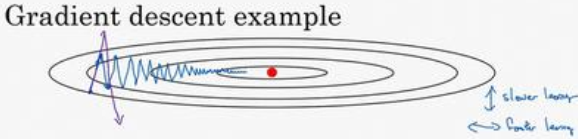
总结来说,我们希望在b方向学习慢一些,减少不必要的摆动,在W方向上加快学习,快速接近最小值。
因此,一个可以的解决方法是,使用动量梯度下降法。在每次迭代过程中,计算微分dW和db,并计算$V_{dW}=\beta V_{dW}+(1-\beta)dW$,同样计算$V_{db}=\beta V_{db}+(1-\beta)db$,并将计算后的值重新赋值给dW和db,这样做有什么好处呢。

类似于上面的图,通过加权平均,将震荡往复的梯度值dW和db转换为连续变化的梯度值,使得在b方向上正负抵消,dW的摆动减小了,W方向上由于所有微分方向一致,因此W方向运动更快了。
可以理解为成本函数是一个碗状函数,梯度下降就是在碗的边缘滚下一个球,$(1-\beta)dW$和$(1-\beta)db$项相当于在每一刻提供一个加速度,$\beta v_{dW}$和$\beta v_{db}$相当于上一时刻的瞬时速度。因此速度会越滚越快,并且由于$\beta$小于1,类似于表现出一些摩擦力,所以球不会无限加速下去。
因此动量梯度下降法过程如下:
$V_{dW}=\beta V_{dW}+(1-\beta)dW$
$V_{db}=\beta V_{db}+(1-\beta)db$
$W=W-\alpha v_{dW}$
$b=b-\alpha v_{db}$
这个过程中超参数有两个:动量$\beta$和学习率$\alpha$
2.3 编程实现
1 | def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate): |
三、RMSprop
RMSprop的全称是root mean square prop算法,也可以加速梯度下降。
数学表示如下:
$S_{dW}=\beta S_{dW}+(1-\beta)dW^2$
$S_{dW}=\beta S_{dW}+(1-\beta)dW^2$
参数更新过程如下:
$W=W-\alpha \frac{dW}{\sqrt{S_{dW}}}$
$b=b-\alpha \frac{db}{\sqrt{S_{db}}}$
原理如下:
我们希望学习速度快,并且要减缓摆动。于是有了$S_{dW}$和$S_{db}$,我们希望$S_{dW}$较小,所以要除以一个较小的数,希望$S_{db}$较大,所以要除以一个较大的数,这样就可以减缓b上的摆动。而且这些微分项里面,由于斜率在b的方向上要大于在W的方向,因此db大一些,dW小一些,$S_{dW}$除以一个较小的数也就是dW$S_{db}$除以一个较小的数也就是db,因此有了上面的式子。
四、Adam
Adam优化算法全称为Adaptive Moment Estimation。是动量梯度下降法Momentum和RMSprop的结合。
具体步骤如下:
$V_{dW}=\beta_1 v_{dW}+(1-\beta_1)dW$
$V_{db}=\beta_1 v_{db}+(1-\beta_1)db$
$S_{dW}=\beta_2 S_{dW}+(1-\beta_2)dW^2$
$S_{dW}=\beta_2 S_{dW}+(1-\beta_2)dW^2$
$W=W-\alpha \frac{V_{dW}}{\sqrt{S_{dW}}+\epsilon}$
$b=b-\alpha \frac{V+{db}}{\sqrt{S_{db}}+\epsilon}$
其中的$\epsilon$常取$10^{-8}$,是为了避免出现除以0的情况,所以附加的微小值。
该算法结合了Momentum和RMSprop两种方法,被证明有效适用于不同的神经网络。
本算法涉及了多个超参数
- $\alpha$:学习率
- $\beta_1$:Momentum相关的项,常用的缺省值为0.9
- $\beta_2$:Adam相关的项,常用的缺省值为0.99
- $\epsilon$:常用$10^{-8}$,该参数对算法没什么影响
编程实现
1 | def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01, |
五、学习率衰减
由于在梯度下降过程中,会围绕最小值往复震荡,但是不会精确的收敛,为了保证算法的效率。可以在初期设置较大的学习率,这样学习相对较快,梯度下降速度较快。接近最小值附近时,减小学习率,也就是减小步伐,逐渐逼近最小值。
因此可以这样操作,每一次遍历所有数据集,都让学习率减小一些。
(1)最常用的衰减公式
$\alpha=\frac{1}{1+decay_rate\times epoch_num}$
其中decay_rate为衰减率,epoch_num为迭代次数。随着epoch_num的增大,学习率$\alpha$会逐渐减小。
(2)指数衰减
$\alpha=0.95^{epoch_num}\cdot\alpha_0$
(3)反比衰减
$\alpha=\frac{k}{\sqrt{epoch_num}}\cdot a_0$