一、数据操作与数据预处理

1.1 数据操作

（1）N维数组

0维，标量，表示一个类别

1
1.0

1维，向量，表示一个特征向量

1
[1.0, 2.7, 3.4]

2维，矩阵，表示一个样本或特征矩阵

1
2
3
[[1.0, 2.7, 3.4]
 [5.0, 0.2, 4.6]
 [4.3, 8.5, 0.2]]

3维，表示一个RGB图片（宽×高×通道）

1
2
3
4
5
6
[[[1.0, 2.7, 3.4]
  [5.0, 0.2, 4.6]
  [4.3, 8.5, 0.2]]
 [[3.2, 5.7, 3.4]
  [5.4, 6.2, 3.2]
  [4.1, 3.5, 6.2]]]

4维，表示一个视频或RGB图片的批量（批量大小×宽×高×通道）

1
2
3
[[[[...
	...
	...]]]]

5维，表示一个视频批量（批量大小×时间×宽×高×通道）

1
2
3
[[[[[...
	 ...
	 ...]]]]]

（2）数组相关

创建数组需要

  1. 形状
  2. 每个元素的数据类型
  3. 每个元素的值

访问元素

  1. 一个元素：[1, 2]
  2. 一行：[1, :]
  3. 一列：[:, 1]
  4. 子域：[1:3, 1:]
  5. 跳跃访问：[::3, ::2]

1.2 数据操作的实现

（1）导入torch

1
import torch

（2）创建张量

1
2
x = torch.arange(10)
# 输出：tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])

（3）获取张量的形状

1
2
x.shape
# 输出：torch.Size([12])

（4）获取张量中元素的个数

1
2
x.numel()
# 输出：12

（5）改变张量的形状

1
X = x.reshape(3, 4)

注意：reshape只是创建了一个浅拷贝，例如
a = torch.arange(6)
b = a.reshape((2,3))
b[:]=2
结果运算过后，a也变成了tensor([2, 2, 2, 2, 2, 2])
相当于b创建了一个a的view，只是用特定的方式观察a，地址空间仍然是同一个。

（6）创建初始化矩阵

1
2
torch.zeros((2, 3, 4))
torch.ones(2, 3, 4)

（7） 将列表转换为张量

1
torch.tensor(list)

（8）张量的标准运算符是按元素运算

1
2
3
4
5
6
7
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y
x - y
x * y
x / y
x ** y

（9）多个张量连在一起

1
2
3
4
X = torch.arange(12).reshape((3, 4))
Y = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim = 0) # 按行堆叠，纵向堆叠
torch.cat((X, Y), dim = 1) # 按列堆叠，横向堆叠

（10）张量元素求和

1
2
X.sum()
# 输出：tensor(66.)

（11）广播机制：形状不同的张量可以通过广播实现按元素运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
'''
a: tensor([[0],
		   [1],
		   [2]])
b: tensor([[0, 1]])
'''
a + b
'''
a+b: tensor([[0, 1],
		     [1, 2],
		     [2, 3]])
'''

（12）转换为numpy张量

1
A = X.numpy() # numpy.ndarray

1.3 数据预处理实现

（1）创建数据集

创建一个人工数据集，并存储在csv逗号分隔值文件

1
2
3
4
5
6
7
8
9
10
import os

os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n')
    f.write('NA,Pave,127500\n')
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

（2）从创建的csv文件中加载原始数据集

1
2
3
4
5
6
# 如果没有安装pandas，只需取消对以下行的注释来安装pandas
# !pip install pandas
import pandas as pd

data = pd.read_csv(data_file)
print(data)

（3）处理缺失数据

常见的方法包括：

  • 将缺失数据的行删除
  • 插值

对于数值数据，进行插值替换

1
2
3
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 1]
inputs = inputs.fillna(inputs.mean()) # 将其他的NaN转换成当前列剩余值的均值
print(inputs)

对于类别值或离散值，我们将NaN视为一个类别，再转换成数值类型

1
2
inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)

（4）数据转换张量

由于读取的数据条目都是数值类型，可以转换为张量格式。

1
2
3
4
import torch

X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, y

二、线性代数的实现

2.1 线性代数

（1）标量

标量，由只有一个元素的张量表示

1
2
3
4
import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

（2）向量

向量是由标量组成的列表

1
x = torch.arange(4)

（3）矩阵

通过二维数组作为矩阵

1
A = torch.arange(20).reshape(5, 4)

矩阵的转职

1
A.T

（4）张量的形状

访问向量的长度

1
len(x)

访问张量的形状

1
x.shape

（5）张量的运算

给定具有相同形状的任何两个张量，任何按元素二元运算的结果都是相同形状的张量

1
2
3
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

计算元素的和

1
2
3
4
x.sum() #直接使用得到的是一个标量，不管矩阵是什么维度都得到标量
A.sum(axis = 0) # 按第0轴求和
A.sum(axis = 1) # 按第1轴求和
A.sum(axis = 2) # 按第2轴求和

对于一个张量，其有三个维度，可以理解为RGB图像的（宽，高，通道数），或者直观理解为一个长方体的（宽，长，高）
其高度方向或者RGB的通道数是最高维度，也就是第0轴。
对于axis=0进行求和，相当于将长方体高度方向压扁，或者将RGB三个通道合成一个通道
对于axis=1进行求和，相当于将长方体长度方向压扁，或者将RGB图像沿每个通道的高方向压扁
对于axis=2进行求和，相当于将长方体宽度方向压扁，或者将RGB图像沿每个通道的宽方向压扁

此外sum方法还有一个keepdims参数，如果为True，那么将在求和时保持维度不变，将被压扁的维度设置为1。（这样方便通过广播实现A/A.sum）

计算平均值

1
2
A.mean
A.mean(axis = 0)

（6）矩阵的乘法

按元素乘

1
A * B

点积是按元素乘积的和

1
2
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)

矩阵乘向量

1
torch.mv(A, x)

矩阵乘矩阵

1
torch.mm(A, B)

（7）范数

L2范数是向量元素平方和的平方根

1
torch.norm(u)

L1范数是向量元素的绝对值之和

1
torch.abs(u).sum()

矩阵的F范数是矩阵元素的平方和的平方根

1
torch.norm(torch.ones(A))

三、矩阵计算

3.1 梯度

梯度是导数从标量拓展到向量的形式

（1）标量对向量的导数

$x = [x_1, x_2, \cdots, x_n].T$

$\frac{\partial y}{\partial \textbf{x}}=[\frac{\partial y}{\partial x_1},\frac{\partial y}{\partial x_2},\cdots,\frac{\partial y}{\partial x_n}]$

例如，对于函数$y=x_1^2+2x_2^2$，其对向量$\textbf x=[x_1, x_2]$的导数是

$\frac{\partial y}{\partial \textbf x} = \frac{\partial x_1^+2x_2^2}{\partial \textbf x}=[2x_1, 4x_2]$

可以直观理解为$y=x_1^2+2x_2^2$是一圈圈椭圆，对于任意给定的$[x_1, x_2]$，都可以找到$[2x_1, 4x_2]$这个方向是$y$下降最快的方向。即梯度就是函数值下降最快的方向。

（2）向量对标量的导数

$y = [y_1, y_2, \cdots, y_n].T$

$\frac{\partial \textbf y}{\partial x}=[\frac{\partial y_1}{\partial x},\frac{\partial y_2}{\partial x},\cdots,\frac{\partial y_n}{\partial x}].T$

即$\frac{\partial y}{\partial \textbf{x}}$是行向量，$\frac{\partial \textbf y}{\partial x}$是列向量。

（3）向量对向量的导数

向量对向量的导数是一个矩阵：

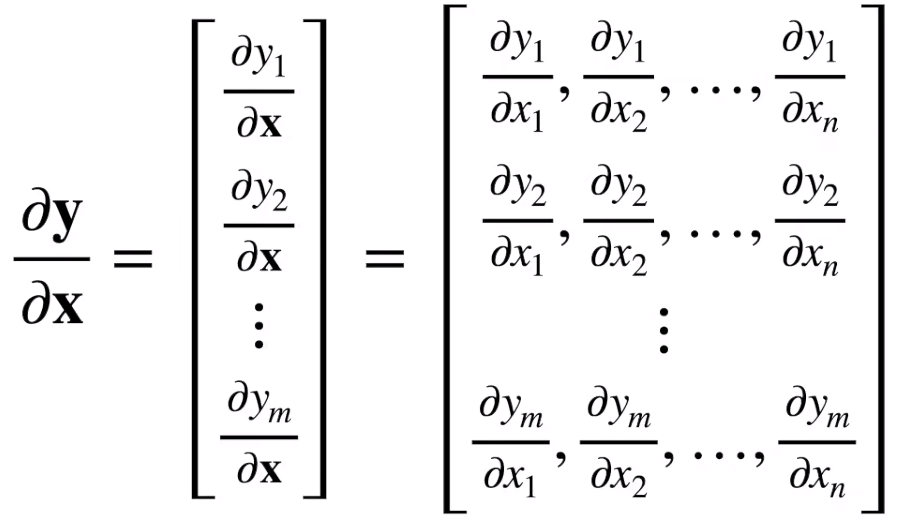
3.2 向量链式法则

标量的链式法则：

$y=f(u),u=g(x)$，则$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x}$

向量的链式法则：

$\frac{\partial y}{\partial \textbf x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial \textbf x}$ (1,n) = (1, )(1, n)

$\frac{\partial y}{\partial \textbf x}=\frac{\partial y}{\partial \textbf u}\frac{\partial \textbf u}{\partial \textbf x}$ (1,n) = (1, k)(k, n)

$\frac{\partial \textbf y}{\partial \textbf x}=\frac{\partial \textbf y}{\partial \textbf u}\frac{\partial \textbf u}{\partial \textbf x}$ (m,n) = (m,k)(k.n)

3.3 自动求导

自动求导是计算一个函数在指定值上的导数。

（1）计算图

计算图是将代码反结成操作子，将计算表示成一个无环图。相当于将函数求导过程使用链式法则求导

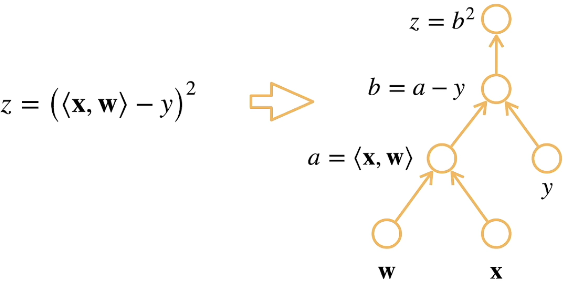
（2）自动求导的模式

链式法则：$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}}\cdots \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x}$

  • 正向积累：$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}(\frac{\partial u_n}{\partial u_{n-1}}(\cdots (\frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x})))$

  • 反向传递：$\frac{\partial y}{\partial x}=(((\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}})\cdots) \frac{\partial u_2}{\partial u_1})\frac{\partial u_1}{\partial x}$

一般对于输入数据会先正向计算结果，再反向计算梯度，正向计算时会保存所有的中间变量。计算梯度的时候已经有了abz的具体值了，直接带入就能得到导数，比如dz/db=2b。同理其它操作子的导数也可以直接带数得到，根据链式法则最终的梯度就是各个操作子导数的乘积。

（3）自动求导的pytorch实现

假设对函数$\textbf y=2\textbf x^T \textbf x$对于列向量$\textbf x$求导

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import torch

# 创建输入
x = torch.arange(4.0)

# 创建一个空间存储梯度值，执行后x.grad就可以存储梯度值，默认为none
x.requires_grad_(True)

# 计算y
y = 2 * torch.dot(x, x)

# 调用反向传播函数计算y关于x每个分量的梯度，结果将自动保存在x.grad中
y.backward()

# 默认情况下，pytorch会累计梯度，如果需要计算其他函数的梯度，需要先清除之前的值
x.grad.zero_()

有时我们需要将某些参数移动到计算图之外：

1
2
3
4
5
6
7
8
9
10
11
# 清空x.grad
x.grad.zero_()

# 定义y
y = x * x

# 将y从计算图中剔除，y的当前结果保存为u，则u=x*x是一个固定的值
u = y.detach()

# 此时u和x无关，u.backward()是0向量
# y仍然和x有关，y.backward()是2 * x

上面的步骤就实现了将y这个参数的当前值保存出来记为u，而y不受影响，在深度学习中会用到这种操作。